Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
The Class 10 is an important year in a student’s life and Maharashtra State Board Class 10 Maths 2 one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 10 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 10 Maths 2 Book syllabus.

Practice set 2.1 Page 38
1. Identify, with reason, which of the following are Pythagorean triplets.
(i)(3, 5, 4)
(ii)(4, 9, 12)
(iii)(5, 12, 13)
(iv) (24, 70, 74)
(v)(10, 24, 27)
(vi)(11, 60, 61)
Solution:
(i)(3, 5, 4)
32 = 9
42 = 16
52 = 25
Here 9+16 = 25
52 = 32 +42
The square of largest number is equal to sum of squares of the other two numbers.
(3, 5, 4) is a Pythagorean triplet.
(ii)(4, 9, 12)
42 = 16
92 = 81
122 = 144
Here 42 +92 ≠ 122
The square of largest number is not equal to sum of squares of the other two numbers.
(4, 9, 12) is not a Pythagorean triplet.
(iii)(5, 12, 13)
52 = 25
122 = 144
132 = 169
Here 52 + 122 = 132
The square of largest number is equal to sum of squares of the other two numbers.
(5, 12, 13) is a Pythagorean triplet.
(iv) (24, 70, 74)
242 = 576
702 = 4900
742 = 5476
Here 242 + 702 = 742
The square of largest number is equal to sum of squares of the other two numbers.
(24, 70, 74)is a Pythagorean triplet.
(v)(10, 24, 27)
102 = 100
242 = 576
272 = 729
Here 102 +242 ≠ 272
The square of largest number is not equal to sum of squares of the other two numbers.
(10, 24, 27) is not a Pythagorean triplet.
(vi)(11, 60, 61)
112 = 121
602 = 3600
612 = 3721
Here 112 +602 = 612
The square of largest number is equal to sum of squares of the other two numbers.
(11, 60, 61)is a Pythagorean triplet.
2. In figure 2.17, MNP = 90°, seg NQ ⊥seg MP, MQ = 9, QP = 4, find NQ.

Solution:
In MNP , MNP = 90˚, seg NQ ⊥ seg MP
MQ = 9 , QP = 4 [Given]
NQ = √(MQ×QP) [Theorem of geometric mean]
NQ = √(9×4) = √36 = 6
Hence NQ = 6 units.
3. In figure 2.18, QPR = 90°, seg PM ⊥seg QR and Q-M-R, PM = 10, QM = 8, find QR.

Solution:
In PQR , QPR = 90˚
seg PM ⊥ seg QR [Given]
PM2 = QM×MR [Theorem of geometric mean]
102 = 8×MR
MR = 100/8 = 12.5
QR = QM + MR
QR = 8+12.5 = 20.5
Hence measure of QR is 20.5 units.
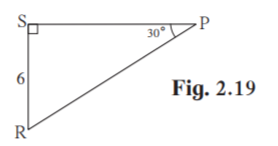
4. See figure 2.19. Find RP and PS using the information given in PSR.
Solution:
In PSR , P = 30˚ , S = 90˚
R = 180 –(90+30) = 60˚ [Angle Sum property of triangle]
PSR is a 30˚ –60˚ –90˚ triangle.
SR = (½)×PR [side opposite to 30˚]
6 = (½)× PR
PR = 12
PS = √(PR2 -SR2 [Pythagoras theorem]
PS = √(122 -62 )
PS = √(144-36)
PS = √108
PS = 6√3
Hence RP = 12 units and PS = 6√3 units.
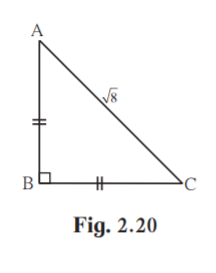
5. For finding AB and BC with the help of information given in figure 2.20, complete following activity.
AB = BC ….____
BAC = _____
AB = BC = ____× AC
= ____ ×√8
= ____ × 2√2
= ____
Solution:
AB = AC [Given ]
BAC = BCA [Angles opposite to equal sides of an isosceles triangle are equal]
AB = BC = 1/√2× AC [By 45˚ –45˚-90˚ theorem]
=(1/√2) ×√8
=(1/√2) × 2√2
= 2
Practice set 2.2 Page 43
1. In PQR, point S is the midpoint of side QR. If PQ = 11,PR = 17, PS =13, find QR.
Solution:
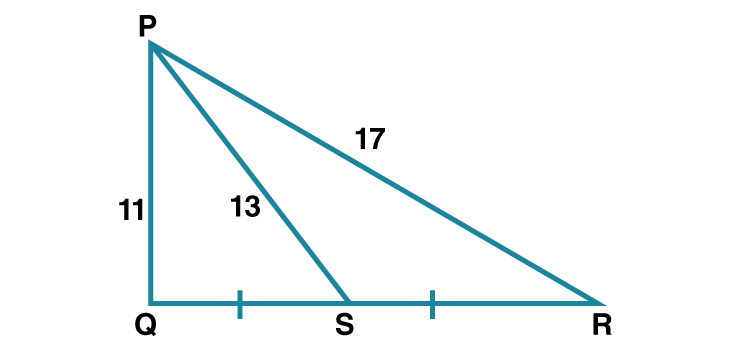
Given , S is the midpoint of QR .
PS is the median.
PQ2 +PR2 = 2 PS2 +2SR2 [By Apollonius theorem]
112 +172 = 2×132 +2×SR2
121+289 = 2×169+2×SR2
2SR2 = 121+289-338
2SR2 = 72
SR2 = 72/2 = 36
SR = 6
Since S is the midpoint of QR , QR = 2SR
QR = 2×6 = 12
Hence QR = 12 units.
2. In ABC, AB = 10, AC = 7, BC = 9 then find the length of the median drawn from point C to side AB
Solution:
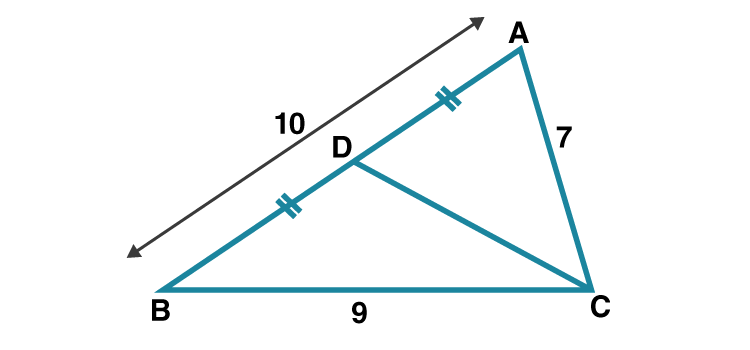
Let CD is the median drawn from C to AB.
Given AB = 10
AD = (1/2)×AB [D is the midpoint of side AB]
AD = 10/2 = 5
Since CD is the median
AC2 +BC2 = 2CD2 +2AD2 [Apollonius theorem]
72 +92 = 2 CD2 +2×52
2 CD2 = 72 +92 -2×52
2 CD2 = 80
CD2 = 40
Taking square roots on both sides
CD = 2√10
Hence the length of median drawn from point C to side AB is 2√10 units.
3. In the figure 2.28 seg PS is the median of PQR and PT ⊥QR. Prove that,
(1) PR2 = PS2 + QR × ST +( QR/ 2 )2
(ii) PQ2 = PS2 –QR ×ST +( QR /2)2
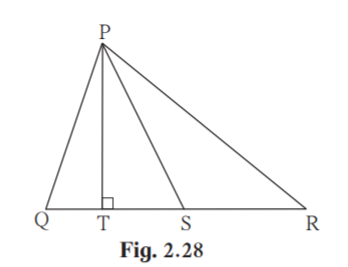
Solution:
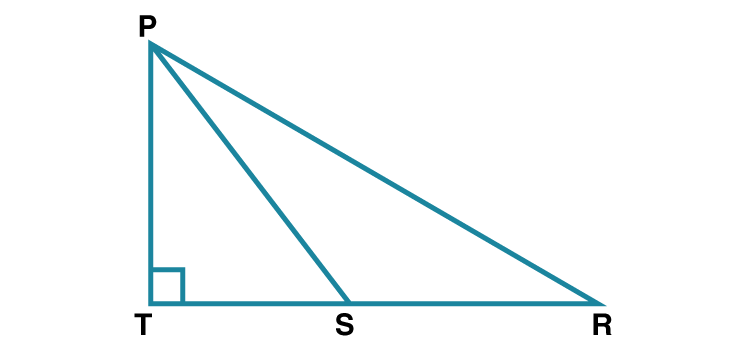
(1) QS = ½ QR ……(i) [S is the midpoint of QR]
SR = ½ QR ……(ii)
QS = SR [From (i) and (ii)]
PT ⊥QR [Given]
PSR is an obtuse angle. [From figure]
PR2 = SR2 +PS2 +2SR×ST …..(iii) [Application of Pythagoras theorem]
Substitute SR = ½ QR in (iii)
PR2 =[(½)QR]2 +PS2 +2(1/2)QR×ST
PR2 =[(½)QR]2 +PS2 +QR×ST
PR2 = PS2 + QR×ST +(QR/ 2 )2
Hence proved.
(ii) PT⊥QS [Given]

PSQ is an acute angle [From figure]
PQ2 = QS2 +PS2 -2QS×ST [Application of Pythagoras theorem]
PR2 = [(1/2)QR]2 +PS2 -2(1/2 )QR×ST
PR2 = (QR/2)2 +PS2 -QR×ST
PR2 = PS2 -QR×ST+( QR /2)2
Hence proved.
Problem set 2 Page 43
1. Some questions and their alternative answers are given. Select the correct alternative.
(1) Out of the following which is the Pythagorean triplet?
(A) (1, 5, 10)
(B) (3, 4, 5)
(C) (2, 2, 2)
(D) (5, 5, 2)
Solution:
(A) (1, 5, 10)
Here 12 +52 ≠ 102
The square of largest number is not equal to sum of squares of the other two numbers.
So (1, 5, 10) is not a Pythagorean triplet.
(B) (3, 4, 5)
Here 32 +42 = 52
The square of largest number is equal to sum of squares of the other two numbers.
So (3, 4, 5) is a Pythagorean triplet.
(C) (2, 2, 2)
Here 22 +22 ≠ 22
The square of largest number is not equal to sum of squares of the other two numbers.
So (2, 2, 2) is not a Pythagorean triplet.
(D) (5, 5, 2)
Here 22 +52 ≠ 52
The square of largest number is not equal to sum of squares of the other two numbers.
So (5, 5, 2) is not a Pythagorean triplet.
Hence option B is the correct answer.
3. In RST, S = 90°, T = 30°, RT = 12 cm then find RS and ST.
Solution:
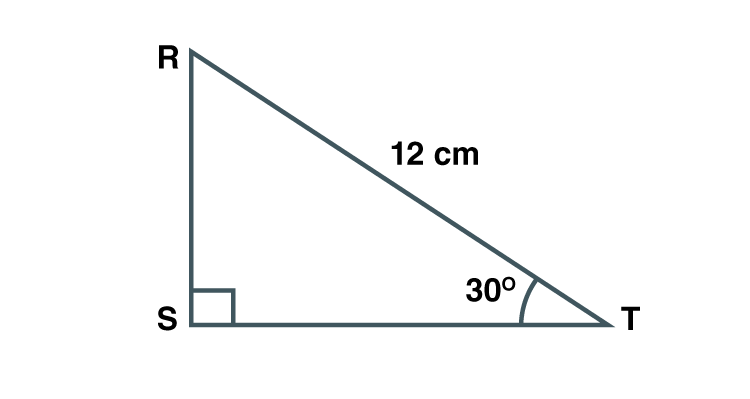
Given S = 90˚ , T = 30˚
R = 180-(90+30) = 60˚ [Sum of angles of triangle is equal to 180˚]
RST is a 30˚ –60˚- 90˚ triangle
RS = ½ RT [Side opposite to 30˚]
RS = ½ ×12 = 6
ST = √3/2 RT [side opposite to 60˚]
ST = (√3/2 )×12
ST = 6√3
Hence RS = 6 cm and ST = 6√3cm.
4. Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm.
Solution:
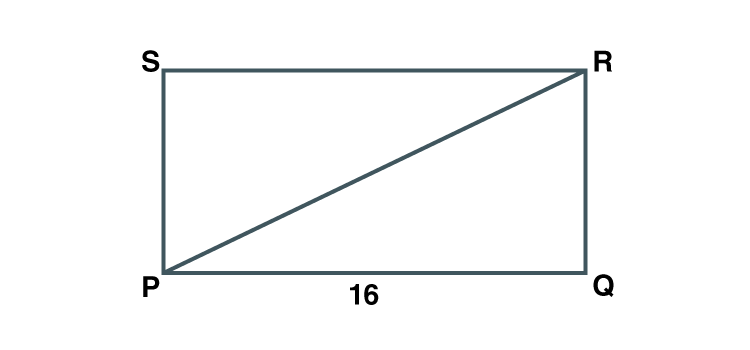
Let PQRS be the rectangle.
Let length be PQ = 16 cm
Area of rectangle = Length × Breadth
Area of rectangle PQRS = PQ×QR
192 = 16×QR
QR = 192/16 = 12cm
Now in PQR , Q = 90˚ [Angles of a rectangle are 90˚]
PR2 = PQ2 +QR2 [Pythagoras theorem]
PR2 = 162 +122
PR2 = 256+144 = 400
PR = 20
Hence the diagonal of the rectangle is 20cm long.
5*. Find the length of the side and perimeter of an equilateral triangle whose height is √3 cm.
Solution:
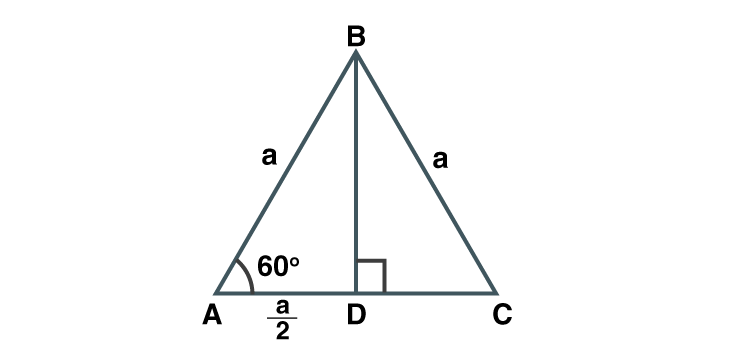
Let ABC be the equilateral triangle with side a.
Let BD be height of the triangle.
Since ABC is equilateral, BD is a perpendicular bisector.
AD = a/2
BD = √3 [given height = √3]
AB = a
Applying Pythagoras theorem in ABD
AB2 = AD2 +BD2
a2 = (a/2)2 +(√3)2
a2 = (a2 /4)+3
(3/4)a2 = 3
a2 = 4
a = 2
Hence length of side of equilateral triangle is 2 cm.
Perimeter = 3×2 = 6 [Perimeter of equilateral triangle = 3×side]
Hence perimeter of equilateral triangle is 6 cm.
6. In ABC seg AP is a median. If BC = 18, AB2 + AC2 = 260 Find AP.
Solution:
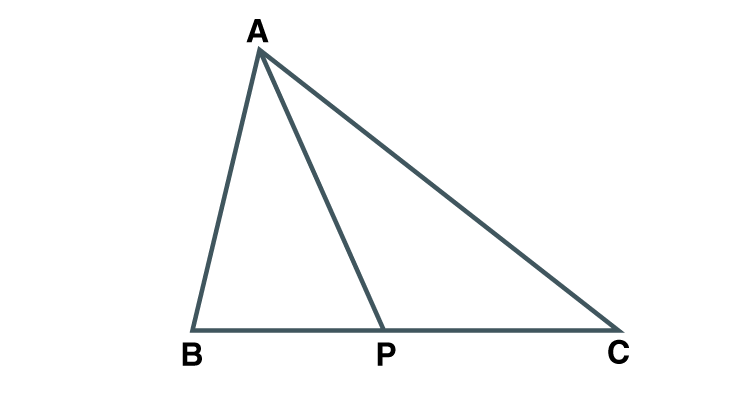
Given AP is the median.
PC = BC/2
PC = 18/2 =9
AB2 +AC2 = 2AP2 +2PC2 [Apollonius theorem]
260 = 2AP2 +2×92
2AP2 = 260-2×92
2AP2 = 260-162
AP2 = 68/2 = 49
Taking square roots on both sides
AP = 7
Hence AP = 7 units.
7*. ABC is an equilateral triangle. Point P is on base BC such that PC = 1/3 BC, if AB = 6 cm find AP.
Solution:
Given ABC is an equilateral triangle.
PC = (1/3) BC
PC = (1/3)×6 [BC = 6, side of equilateral triangle]
PC = 2
Construction:
Draw segment AD⊥BC

In ADC, C = 60˚
D = 90˚
CAD = 30˚
ADC is a 30˚- 60˚- 90˚triangle
AD = (√3/2)×AC [Side opposite to 60˚]
AD = (√3/2)×6
AD =3√3cm
DC = (1/2)BC [AD⊥BC]
DC = (1/2)×6 = 3cm
DC = DP+PC [D-P-C]
3 = DP +2
DP = 1
In ADP , D = 90˚
Applying Pythagoras theorem
AP2 = AD2 +DP2
AP2 = (3√3)2 +12
AP2 = 28
AP = 2√7 cm
Hence AP = 2√7cm.
8. From the information given in the figure 2.31, prove that PM = PN = √3 ×a
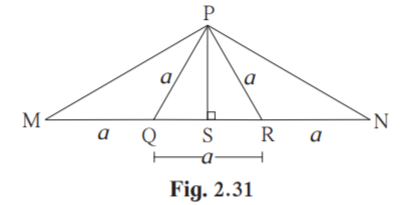
Solution:
Proof:
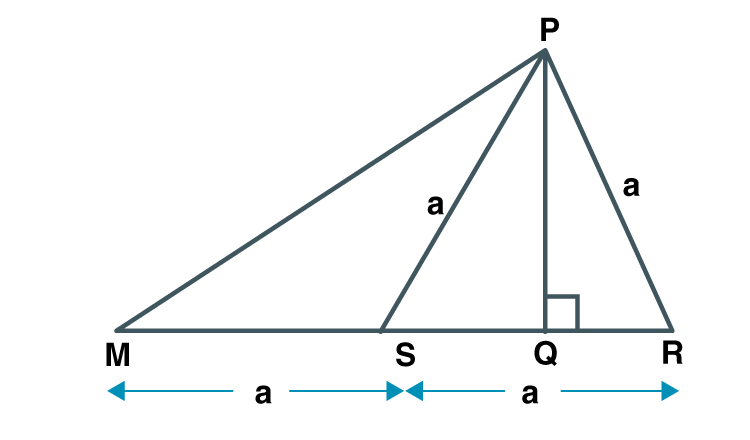
In PRM
Given MQ = QR = a
Q is the midpoint of MR .
PQ is the median.
PR2 +PM2 = 2PQ2 +2QM2 [Apollonius theorem]
a2 +PM2 = 2a2 +2a2
PM2 = 3a2
PM = √3a…………(i)
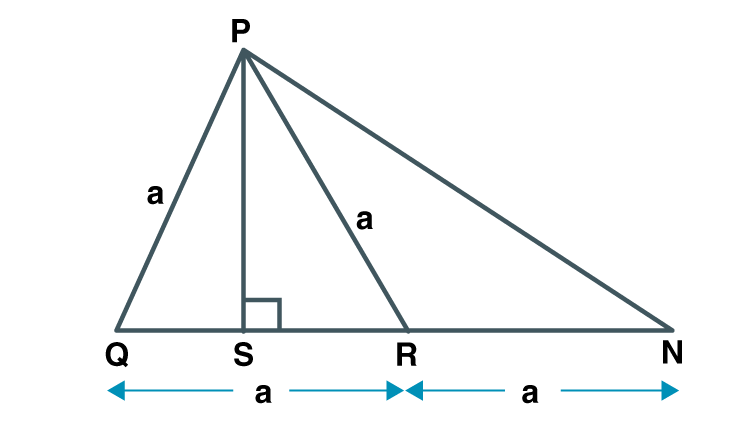
In PQN
Given NR = QR = a
R is the midpoint of QN.
PR is the median.
PN2 +PQ2 = 2PR2 +2RN2 [Apollonius theorem]
PN2 +a2 = 2a2 +2a2
PN2 = 3a2
PN = √3a…………..(ii)
From (i) and (ii) PM = PN = √3×a
Hence proved.
9. Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
Solution:
Construction:
Draw a parallelogram ABCD. Let diagonals AC and BD meet at P.
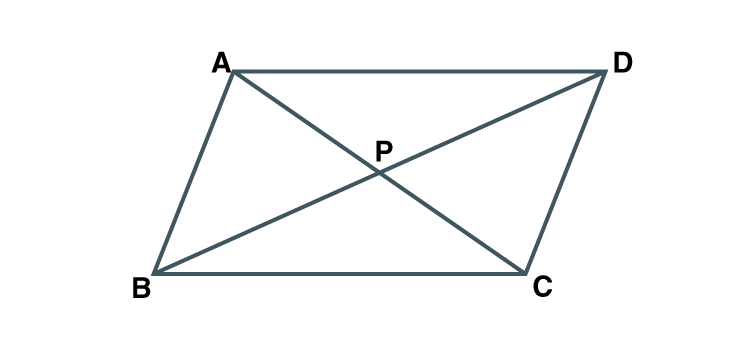
To prove : AC2 +BD2 = AB2 +BC2 +CD2 +DA2
AB = CD [Opposite sides of parallelogram are equal]
BC = DA [Opposite sides of parallelogram are equal]
Since diagonals of a parallelogram bisect each other,
AP = ½ AC
BP = ½ BD
P is the midpoint of diagonals AC and BD.
InABC , BP is the median.
AB2 +BC2 = 2AP2 +2BP2 [Apollonius theorem]
AB2 +BC2 = 2[(1/2)AC]2 +2[(1/2)BD]2
AB2 +BC2 =AC2 /2+BD2 /2
2(AB2 +BC2 ) = AC2 +BD2
2AB2 +2BC2 = AC2 +BD2
AB2 + AB2 + BC2 +BC2 = AC2 +BD2
AB2 + CD2 + BC2 +DA2 = AC2 +BD2
AC2 +BD2 = AB2 +BC2 +CD2 +DA2
Hence proved.
10. Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was 15√2 km. Find their speed per hour.
Solution:
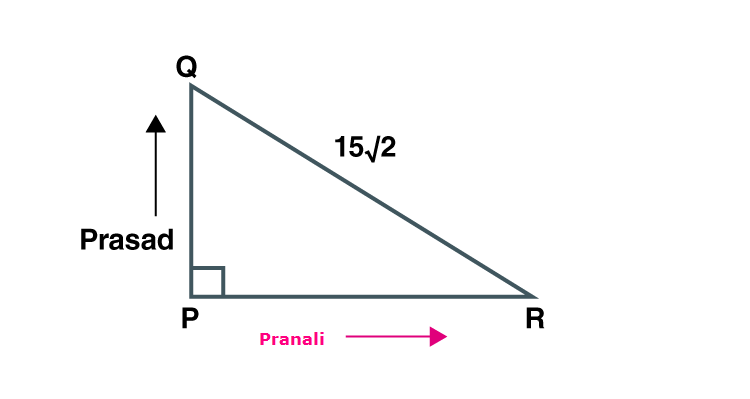
Distance between Pranali and Prasad after 2 hours = 15√2 km
Since they travel at same speed, they have covered same distance.
Construction: Draw a triangle PQR such that PQ = PR = x and QR = 15√2
P = 90˚
In PQR , PQ2 +PR2 = QR2 [Pythagoras theorem]
x2 +x2 = (15√2)2
2x2 = 2×225
x2 = 225
x = 15
Distance covered by them is 15 km.
Given time = 2 hours
Speed = Distance / time
Speed = 15/2 = 7.5km/hr
Speed of Pranali and Prasad is 7.5km/hr.
Pythagoras theorem is the fundamental theorem in Mathematics, which defines the relation between the hypotenuse, base and altitude of a right angled triangle. According to this theorem, the square of hypotenuse is equal to the sum of squares of altitude and base of a right angled triangle. Apollonius theorem is also explained in this chapter. Pythagoras Theorem and solutions.